算法导轮之B树的学习

最近学习了算法导轮里B树相关的知识，在此写一篇博客作为总结。

引言

B树是为磁盘或其他直接存取的辅助存储设备而设计的一种平衡搜索树。B树类似于红黑树，但它与红黑树最大不同之处在于B树的节点可以拥有很多孩子，因此B树的高度会比红黑树小很多，也因此B树在磁盘I/O方面表现要比红黑树好。（对于磁盘操作最耗时的部分在于磁盘读写，而每次读取一个新的树的节点就必须进行一次磁盘读取，因此节点较大、树高度较小的B树会进行较少的磁盘I/O操作）

B树的定义

一颗B树的定义如下：
每个节点x均有如下属性：

1. n表示存储在该节点的关键字个数
2. n个关键字本身key1、key2……keyn以非降序存放，即key1 <= key2 <= …… <= keyn
3. 一个leaf布尔值表示该节点是否为叶节点
4. 每个内部节点包含了n+1个孩子，叶节点没有孩子
5. 关键字keyi对存储在各子树中的关键字范围加以分割：即比keyi小的元素在其左子树，比keyi大的元素在其右子树
6. 每个叶节点具有相同的深度
7. 每个节点包含的关键字个数有上界与下界。我们定义B树的最小度数为t，则除根节点外的每个节点至少有t-1个关键字，每个节点最多有2t-1个关键字（即每个节点最少有t个孩子，最多有2t个孩子）（当一个节点有2t-1个关键字时，我们称它为满的）。

B树的示意图如下：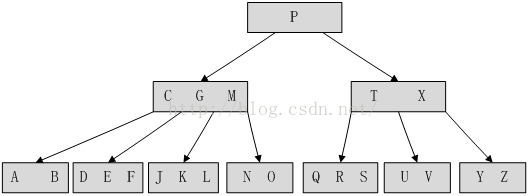

上图是一个最小度数为2的B树，因此每个节点拥有1个、2个或3个元素，拥有2个、3个或4个孩子，也被称为2-3-4树。
根节点只有一个元素，因此它拥有两个孩子；两个孩子分别拥有3个和2个元素，因此他们分别拥有4个和3个孩子。
看到DEF叶节点位于关键字C与G的中间，表明了关键字对于存储在各子树中的关键字范围进行了分割，其余同理。

B树的插入

要讲到树，就不得不提树中关键的插入与删除操作，这里我们先总结B树的插入操作。
当我们往B树中插入一个新的关键字时，由于B树节点的关键字是受到限制的，因此当一个节点关键字数目为2t-1时（该节点是满的），我们就必须进行分裂操作。

分裂节点

分裂节点的主要操作为把满节点的中间关键字提升至父节点，把原满节点分裂为中间关键字的两个左右节点
其示意图如下：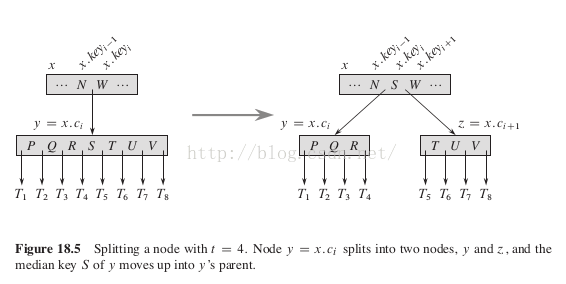

对于某个非满的节点x，若其孩子节点x.ci为满的（即孩子节点的关键字数目为2t-1)。则把其孩子节点的中间关键字（S）提升为父节点（x节点）的关键字，并把原孩子节点（x.c节点）分成两个t-1个关键字的节点，分别位于中间关键字（S）的左、右。
还有一种比较特殊的情况就是B树根的分裂：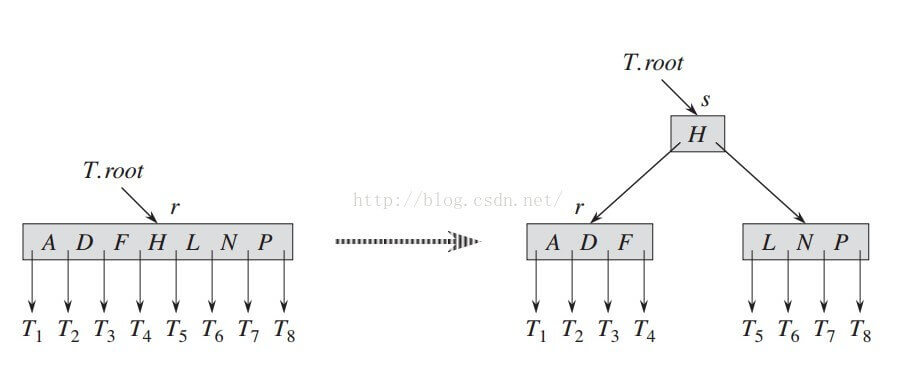

分裂是B树长高的唯一途径，因此分裂是非常重要的。

插入

讲完分裂操作再讲插入操作就非常简单了。插入的时候我们通过比较不断地根据关键字的值寻找孩子节点，当发现一个满的节点时便分裂，最后找到对应的叶节点时根据关键字的值插入相应位置即可。
下面是一个插入关键字的例子：

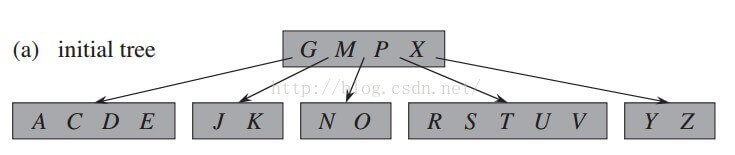
B树的初始状态如图所示，这是一颗最小度数为3的B树，即他的关键字个数为2～5个。

插入关键字B，在根节点由于（B < G）往进入G的左节点，到达叶节点后添加至A与C关键字之间。

插入关键字Q：
在根节点，由于P < Q 而且 Q < X，进入P与X之间的子节点
发现该子节点是满的，则进行分裂，把关键字T上升到父节点，原子节点分为RS与UV，分为在T关键字的左右
由于Q < T，于是进入T的左子节点
在RS叶节点中找到对应位置并加入

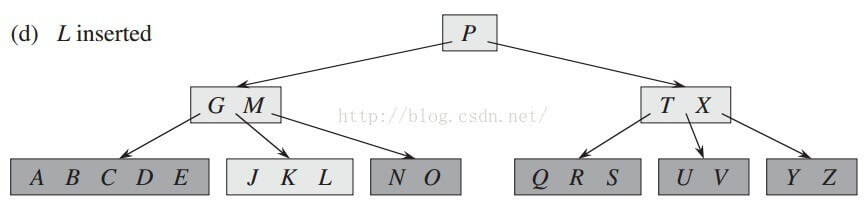
插入关键字L：
发现根节点是满的，分裂根节点，上移P
L < P 进入P的左子节点
G < L < M，进入G与M关键字间的节点
在叶节点的相应位置中插入

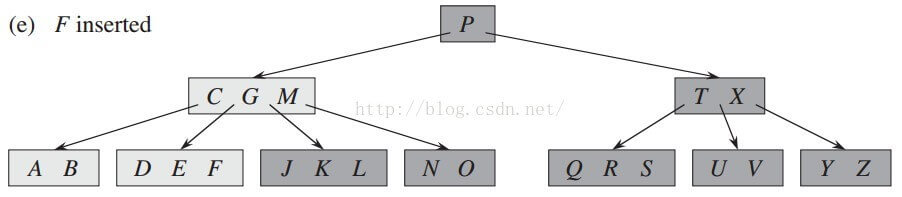
插入关键字F：
F < P，进入P的左子节点
F < G，进入G的左子节点
发现满的节点，分裂，上移C
F > C，进入C的右子节点
在叶节点的相应位置中插入

B树的删除

讲完了B树的插入操作，我们再来讲讲B树的删除操作。
对于删除操作，我们必须保证每个节点在删除前必须至少有t（最小度数）个关键字。

首先我们把要删除的关键字（假设为k）分两种情况：

1. 关键字k在叶节点中：直接删除
2. 关键字k在内部节点中，分三种情况：
   1. k的左子节点拥有t个关键字，则把k的左子节点的最后一个关键字（假设为j）上移到父节点，然后递归的删除j
   2. k的右子节点拥有t个关键字，则把k的右子节点的第一个关键字（假设为l）上移到父节点，然后递归的删除l
   3. k的左右子节点都只有t-1个关键字，则把k下降与左右子节点合并成一个拥有2t-1个关键字的节点，然后递归的删除k

然后我们再定义一些在寻找删除节点路上的操作：如果在寻找删除节点的路上，我们发现某个节点关键字数只有t-1个关键字，则分两种情况：

1. 看该节点的相邻兄弟节点是否含有至少t个关键字，如果是则向相邻的兄弟节点“借一个关键字”（以该节点的左节点为例：把左节点的最后一个关键字上升至父节点，然后父节点位置的节点下移到关键字个数为t-1的节点上）
2. 如果该节点相邻的兄弟节点都只含有t-1个关键字，则选择一个兄弟节点合并，并把两兄弟之间的父节点下移

下面我们来看一个B树删除的例子：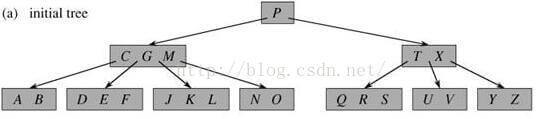

B树的初始状态如图，这是一颗最小度数为3的B树，即每个节点拥有2～5个关键字。

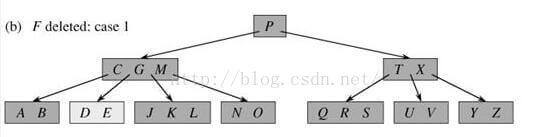
删除F操作：
F < P，进入P的左子节点
C < F < G，进入C与G之间的子节点
在叶节点中删除F

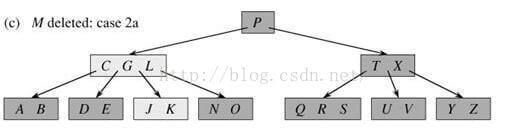
删除M操作：
M < P，进入P的左子节点
在内部节点中发现M，查看M的左子节点JKL，拥有3个关键字，则把最后一个关键字L上升至M的位置，递归的删除L
节点JKL是叶节点，直接删除L即可

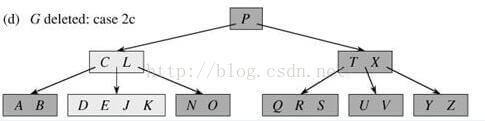
删除G操作：
G < P，进入P的左子节点
在内部节点中发现G，查看G的左右子节点均只有2个关键字（不足最小度数3个），下降G关键字并合并其左右子节点
节点DEGJK为叶节点，直接删除G即可

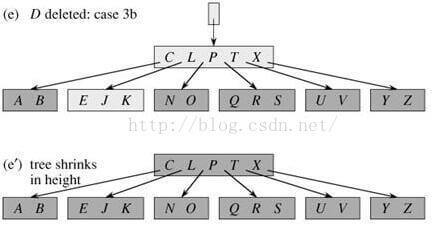
删除D操作：
D < P，进入P的左子节点
发现内部节点CL只有2个关键字（不足最小度数3个），其兄弟节点也只有2个关键字，下降父节点P，与兄弟节点一起合并成一个节点
由于C < D < L，进入C与L间的子节点
DEJK节点是叶节点，直接删除D即可

删除B操作：
B < C，进入E的左子节点
发现节点AC只有两个关键字，其兄弟节点EJK有三个关键字，则E上移到父节点，C下移到子节点，变为节点ABC
节点ABC为叶节点，直接删除B即可