KMP算法小结

发表于 | 分类于
字数统计: 1.1k字

最近看了一些关于KMP算法的资料，在此写一篇博客总计一下。

KMP算法介绍

KMP算法是一种字符串搜索的改进算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

举个例子：
有两个字符串，我们要在第一个字符串（主串）中寻找第二个字符串（模式串）：

ｂａｃｂａｂａｂａｂａｃａａｂ
ａｂａｂｃａ

寻找的方法很简单，就是逐位进行比较，要是不相等就把模式串右移。
考虑下面这种情况：

ｂａｃｂａｂａｂａ ｂａｃａａｂ
　　　　ａｂａｂａ ｃａ

粗体的字符串表示匹配的部分，斜体的字符串表示不匹配的部分。
此时我们的字符串并没有完全匹配，因此我们需要把模式串往右移。

此时一般的字符串匹配算法会这么做：

ｂａｃｂａｂａｂａｂａｃａａｂ
　　　　　ａｂａｂａｃａ　　

但这么做就浪费了我们绿色部分匹配所获得的信息。我们可以看到，对于粗体匹配部分，我们拥有两个相同的前缀与后缀：

后缀：ａｂａｂａ
前缀：　　ａｂａｂａ

因此在这里我们的模式串是可以向右移动两位的：

ｂａｃｂａｂａｂａｂａｃａａｂ
　　　　　　ａｂａｂａｃａ　　

这也就是KMP算法的思想：利用匹配失败后的信息，尽量减少模式串与主串的匹配次数

因此我们会在KMP算法中维护一个next数组，该数组的下标表示了主串与模式串匹配相同的长度（也就是粗体部分字符串的长度，同时也是匹配失败的位置），而数组中则存储了该粗体字符串相同前后缀的长度。因此当我们匹配失败时我们可以移动：粗体字符串长度 - 粗体字符串前后缀长度（如上面的例子就是5 - 3 = 2）

KMP算法的实现

要想实现KMP算法，我们先得把关键的next数组计算出来。计算next数组的方法如下图所示：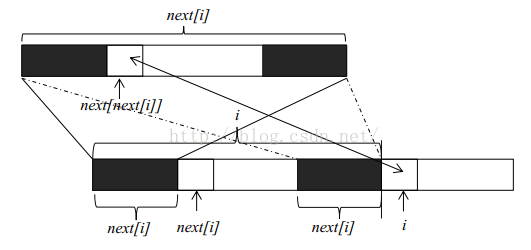
next数组示意图

假设我们要求next[i+1]，那么我们考虑模式串的最后一个字符，即第i位字符。
如果第i位字符与第next[i]位字符相等，那么显而易见next[i+1]的值就是next[i]+1。
但如果第i位字符与第next[i]位字符不等，那么我们就必须寻找字符串前缀中的前缀，就必须比较第i位字符与第next[next[i]]位字符了，直到前缀为0则停止比较。（此处确实绕口……）
因此，根据上面的思想我们可以写出如下Java代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/** 
 * 输入模式字符串返回其对应的next数组 
 * @param p 模式字符串 
 * @return next数组 
 */  
private static int[] KMPNext(String p) {  
    // 初始化  
    int len = p.length();  
    int next[] = new int[len];  
    next[0] = next[1] = 0;  
      
    for (int i = 1; i < len-1; i++) {  
        int j = next[i]; // 相同前缀的最后一位字符  
        while (j > 0 && p.charAt(i) != p.charAt(j)) // 如果第i位字符与前缀最后一位字符不相等，则去寻找前缀的前缀，如果没有前缀则退出循环  
            j = next[j];  
        if (p.charAt(i) == p.charAt(j)) // 如果相等，则最长前后缀长度加一  
            next[i+1] = j+1;  
    }  
      
    return next;  
}

有了next数组，我们就可以写出KMP算法了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/** 
 * KMP搜索字符串 
 * @param m 主字符串 
 * @param p 模式串 
 * @param next next数组 
 */  
private static void KMP(String m, String p, int next[]) {  
    int j = 0; // 模式串索引  
    for (int i = 0; i < m.length(); i++) {  
        while (j > 0 && m.charAt(i) != p.charAt(j)) // 字符不相等，模式串右移，由于字符串已有next[i]个相同的前后缀，因此比较索引为next[i]的字符串即可  
            j = next[j];  
        if (m.charAt(i) == p.charAt(j)) // 字符相等，索引加一   
            j++;  
        if (j == p.length()) { // 已找到结果  
            System.out.println("find the string in " + (i - j + 1));  
            break;  
        }  
    }  
}

最后附上检测用的例子：

1
2
3
4
5
6
public static void main(String[] args) throws Exception {  
    String m = "ｂａｃｂａｂａｂａｂａｃａａｂ";  
    String p = "ａｂａｂａｃａ";  
    int next[] = KMPNext(p);  
    KMP(m, p, next);  
}

结果如下：
程序运行结果